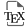Liminal reciprocity and factorization statistics

Hyde, Trevor

Algebraic Combinatorics, Tome 2 (2019) no. 4, pp. 521-539.

Let $M_{d,n}\left(q\right)$ denote the number of monic irreducible polynomials in ${𝔽}_q[x_1,x_2,...,x_n]$ of degree $d$. We show that for a fixed degree $d$, the sequence $M_{d,n}\left(q\right)$ converges coefficientwise to an explicitly determined rational function $M_{d,\infty }\left(q\right)$. The limit $M_{d,\infty }\left(q\right)$ is related to the classic necklace polynomial $M_{d,1}\left(q\right)$ by an involutive functional equation we call liminal reciprocity. The limiting first moments of factorization statistics for squarefree polynomials are expressed in terms of symmetric group characters as a consequence of liminal reciprocity, giving a liminal analog of a result of Church, Ellenberg, and Farb.

Classification : 11T55, 11C08, 11T06
Mots clés : necklace polynomial, finite fields, reciprocity

[1] Bodin, A. Number of irreducible polynomials in several variables over finite fields, Am. Math. Mon., Volume 115 (2008), pp. 653-660 | DOI | MR | Zbl

[2] Carlitz, L. The arithmetic of polynomials in a Galois field, Proc. Natl. Acad. Sci. U.S.A., Volume 17 (1931), pp. 120-122 | DOI | Zbl

[3] Carlitz, L. The arithmetic of polynomials in a Galois field, Am. J. Math., Volume 54 (1932), pp. 39-50 | DOI | MR | Zbl

[4] Carlitz, L. The distribution of irreducible polynomials in several indeterminates, Illinois J. Math., Volume 7 (1963), pp. 371-375 | DOI | MR | Zbl

[5] Carlitz, L. The distribution of irreducible polynomials in several indeterminates II, Canad. J. Math., Volume 17 (1965), pp. 261-266 | DOI | MR | Zbl

[6] Church, T.; Ellenberg, J.; Farb, B. Representation stability in cohomology and asymptotics for families of varieties over finite fields, Algebraic Topology: Applications and New Directions (Contemp. Math.), Volume 620, American Mathematical Society, 2014, pp. 1-54 | MR | Zbl

[7] Cohen, S. D. The distribution of irreducible polynomials in several indeterminates over a finite field, P. Edinburgh Math. Soc., Volume 16 (1968), pp. 1-17 | DOI | MR | Zbl

[8] Hou, X.-D.; Mullen, G. Number of irreducible polynomials and pairs of relatively prime polynomials in several variables over finite fields, Finite Fields Appl., Volume 15 (2009), pp. 304-331 | DOI | MR | Zbl

[9] Hyde, T. Cyclotomic factors of necklace polynomials (2018) (https://arxiv.org/abs/1811.08601)

[10] Hyde, T. Polynomial factorization statistics and point configurations in ${ℝ}^3$, Int. Math. Res. Not. (2018) | DOI

[11] Hyde, T.; Lagarias, J. C. Polynomial splitting measures and cohomology of the pure braid group, Arnold. Math. J., Volume 3 (2017), pp. 219-249 | DOI | MR | Zbl

[12] Metropolis, N.; Rota, G.-C. Witt vectors and the algebra of necklaces, Adv. Math., Volume 50 (1983), pp. 95-125 | DOI | MR | Zbl

[13] Rosen, M. Number theory in function fields, Graduate Texts in Mathematics, 120, Springer Science & Business Media, New York, 2013

[14] Sloane, N. J. A. The On-Line Encyclopedia of Integer Sequences, 2018 (https://oeis.org/A088996, Accessed: 11-29-2018) | Zbl

[15] Stanley, R. P. Combinatorial reciprocity theorems, Adv. Math., Volume 14 (1974), pp. 194-253 | DOI | MR | Zbl

[16] von zur Gathen, J.; Viola, A.; Ziegler, K. Counting reducible, powerful, and relatively irreducible multivariate polynomials over finite fields, Siam J. Discrete Math., Volume 27 (2013), pp. 855-891 | DOI | MR | Zbl

[17] Wan, D. Zeta functions of algebraic cycles over finite fields, Manuscripta Math., Volume 74 (1992), pp. 413-444 | DOI | MR | Zbl